2633. Через точку M
проведены две прямые. Одна из них касается некоторой окружности в точке A
, а вторая пересекает эту окружность в точках B
и C
, причём BC=7
и BM=9
. Найдите AM
.
Ответ. 12 или 3\sqrt{2}
.
Указание. Воспользуйтесь теоремой о касательной и секущей. Рассмотрите два случая.
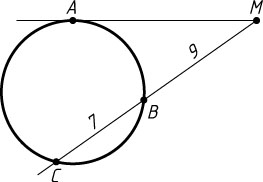
Решение. Пусть точка B
лежит между точками M
и C
. По теореме о касательной и секущей
AM^{2}=MC\cdot MB=(9+7)9=16\cdot9=12^{2}.
Следовательно, AM=12
.
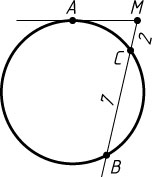
Если точка C
лежит между точками B
и M
, то аналогично получим, что AM=3\sqrt{2}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.4, с. 93

