2634. Радиусы двух концентрических окружностей относятся как 1:2
. Хорда большей окружности делится меньшей окружностью на три равные части. Найдите отношение этой хорды к диаметру большей окружности.
Ответ. \frac{3\sqrt{6}}{8}
.
Указание. Примените теорему о произведениях отрезков пересекающихся хорд.
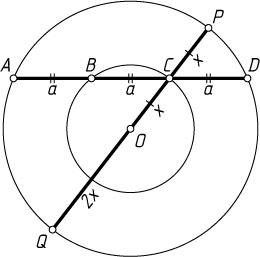
Решение. Пусть хорда AD
большей окружности с центром O
пересекает меньшую окружность в точках B
и C
(B
между A
и C
). Рассмотрим диаметр PQ
большей окружности, проходящий через точку C
(C
между O
и P
). Обозначим OC=x
, AB=BC=CD=a
. Тогда
CD\cdot AC=PC\cdot CQ,~\mbox{или}~a\cdot2a=x\cdot3x,
откуда \frac{a}{x}=\sqrt{\frac{3}{2}}
. Следовательно,
\frac{AD}{PQ}=\frac{3a}{4x}=\frac{3}{4}\cdot\frac{a}{x}=\frac{3}{4}\sqrt{\frac{3}{2}}=\frac{3\sqrt{6}}{8}.