2635. Точка M
лежит внутри окружности радиуса R
и удалена от центра на расстояние d
. Докажите, что для любой хорды AB
этой окружности, проходящей через точку M
, произведение AM\cdot BM
одно и то же. Чему оно равно?
Ответ. R^{2}-d^{2}
.
Указание. Проведите диаметр через точку M
и примените теорему о произведениях отрезков пересекающихся хорд.
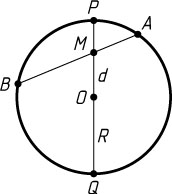
Решение. Пусть O
— центр окружности, R
— радиус, PQ
— диаметр, проходящий через точку M
(M
между O
и P
). По теореме о произведениях отрезков пересекающихся хорд для любой хорды AB
, проходящей через точку M
,
AM\cdot BM=PM\cdot QM=(OP-OM)(OQ+OM)=(R-d)(R+d)=R^{2}-d^{2}.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 128-130
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 273, с. 26
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 8, с. 5
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.6, с. 93
