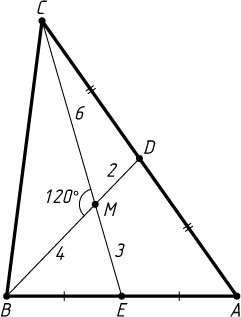
2654. Медианы треугольника ABC
, проведённые из вершин B
и C
, равны 6 и 9 и пересекаются в точке M
. Известно, что \angle BMC=120^{\circ}
. Найдите стороны треугольника.
Ответ. 4\sqrt{7}
; 2\sqrt{13}
; 2\sqrt{19}
.
Указание. Пусть BD
и CE
— медианы треугольника ABC
. Тогда BM=\frac{2}{3}BD
, CM=\frac{2}{3}CE
.
Решение. Пусть BD
и CE
— медианы треугольника ABC
. Тогда
BM=\frac{2}{3}BD=4,~CM=\frac{2}{3}CE=6.
По теореме косинусов из треугольников MBC
, BME
и CMD
находим, что
BC^{2}=BM^{2}+CM^{2}-2BM\cdot CM\cos\angle120^{\circ}=16+36+24=76,
BE^{2}=BM^{2}+EM^{2}-2BM\cdot EM\cos\angle60^{\circ}=16+9-12=13,
DC^{2}=DM^{2}+CM^{2}-2DM\cdot CM\cos\angle60^{\circ}=4+36-12=28.
Следовательно,
BC=\sqrt{76}=2\sqrt{19},~AB=2BE=2\sqrt{13},~AC=2CD=2\sqrt{28}=4\sqrt{7}.