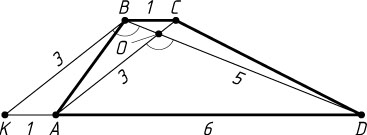
2657. Основания трапеции равны 1 и 6, а диагонали — 3 и 5. Под каким углом видны основания из точки пересечения диагоналей?
Ответ. 120^{\circ}
.
Указание. Через вершину B
меньшего основания BC
трапеции ABCD
проведите прямую, параллельную диагонали AC
. Далее примените теорему косинусов.
Решение. Пусть диагонали AC
и BD
трапеции ABCD
пересекаются в точке O
и равны соответственно 3 и 5, а основания BC
и AD
равны соответственно 1 и 6. Через вершину B
проведём прямую, параллельную диагонали AC
. Пусть эта прямая пересекается с прямой AD
в точке K
. Тогда AKBC
— параллелограмм, значит,
BK=AC=3,~\angle AOD=\angle KBD,~AK=BC=1,~DK=AK+AD=1+6=7.
По теореме косинусов
\cos\angle KBD=\frac{BK^{2}+BD^{2}-DK^{2}}{2BK\cdot BD}=\frac{9+25-49}{2\cdot3\cdot5}=-\frac{1}{2}.
Следовательно,
\angle AOD=\angle KBD=120^{\circ}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.9, с. 30
