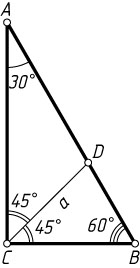
2668. Найдите гипотенузу прямоугольного треугольника с острым углом, равным 30^{\circ}
, если известно, что биссектриса, проведённая из вершины прямого угла, равна a
.
Ответ. \frac{a(\sqrt{6}+3\sqrt{2})}{3}
.
Указание. Воспользуйтесь теоремой синусов.
Решение. Пусть CD
— биссектриса прямоугольного треугольника ABC
, проведённая из вершины C
прямого угла, \angle A=30^{\circ}
, CD=a
. Из треугольника CBD
по теореме синусов находим, что
\frac{BD}{\sin\angle BCD}=\frac{CD}{\sin\angle B},
откуда
BD=\frac{CD\sin\angle BCD}{\sin\angle B}=\frac{a\sin45^{\circ}}{\sin60^{\circ}}=\frac{a\sqrt{2}}{\sqrt{3}}.
Аналогично из треугольника CAD
находим, что AD=a\sqrt{2}
. Следовательно,
AB=BD+AD=\frac{a\sqrt{2}}{\sqrt{3}}+a\sqrt{2}=\frac{a(\sqrt{6}+3\sqrt{2})}{3}.