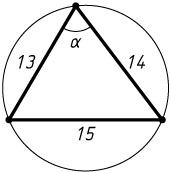
2669. Найдите радиус окружности, описанной около треугольника со сторонами 13, 14, 15.
Ответ. \frac{65}{8}
.
Указание. Найдите синус какого-нибудь угла треугольника и воспользуйтесь обобщённой теоремой синусов.
Решение. Пусть \alpha
— угол, противолежащий стороне, равной 15. Тогда по теореме косинусов
\cos\alpha=\frac{169+196-225}{2\cdot13\cdot14}=\frac{5}{13}.
Следовательно, если R
— радиус окружности, описанной около данного треугольника, то
R=\frac{15}{2\sin\alpha}=\frac{15}{2\sqrt{1-\left(\frac{5}{13}\right)^{2}}}=\frac{15}{2\cdot\frac{12}{13}}=\frac{65}{8}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 80
