2671. Медиана AM
треугольника ABC
равна m
и образует со сторонами AB
и AC
углы \alpha
и \beta
соответственно. Найдите эти стороны.
Ответ. \frac{2m\sin\beta}{\sin(\alpha+\beta)}
, \frac{2m\sin\alpha}{\sin(\alpha+\beta)}
.
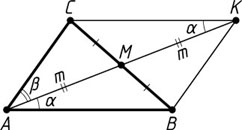
Указание. На продолжении медианы AM
за точку M
отложите отрезок MK
, равный AM
, и примените теорему синусов к треугольнику ACK
.
Решение. На продолжении медианы AM
за точку M
отложим отрезок MK
, равный AM
. Тогда четырёхугольник ABKC
— параллелограмм, поэтому \angle AKC=\angle BAM=\alpha
. Рассмотрим треугольник ACK
. По теореме синусов
\frac{CK}{\sin\beta}=\frac{AK}{\sin(180^{\circ}-\alpha-\beta)},
откуда
AB=CK=\frac{AK\sin\beta}{\sin(\alpha+\beta)}=\frac{2m\sin\beta}{\sin(\alpha+\beta)}.
Аналогично,
AC=\frac{AK\sin\alpha}{\sin(\alpha+\beta)}=\frac{2m\sin\alpha}{\sin(\alpha+\beta)}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 2.1, с. 17
