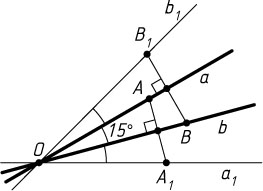
2710. Один из углов, образованных пересекающимися прямыми a
и b
, равен 15^{\circ}
. Прямая a_{1}
симметрична прямой a
относительно прямой b
, а прямая b_{1}
симметрична прямой b
относительно a
. Найдите углы, образованные прямыми a_{1}
и b_{1}
.
Ответ. 45^{\circ}
, 45^{\circ}
, 135^{\circ}
, 135^{\circ}
.
Решение. Возьмём на прямых a
и b
, пересекающихся в точке O
, соответственно точки A
и B
, отличные от O
. Пусть \angle AOB=15^{\circ}
. Точка A_{1}
, симметричная точке A
относительно прямой b
, лежит на прямой a_{1}
, причём
\angle A_{1}OB=\angle AOB=15^{\circ}.
Точка B_{1}
, симметричная точке B
относительно прямой a
, лежит на прямой b_{1}
, причём
\angle B_{1}OA=\angle BOA=15^{\circ}.
Поскольку луч OB
лежит между лучами OA_{1}
и OA
, а луч OA
— между OB
и OB_{1}
, то
\angle A_{1}OB_{1}=\angle A_{1}OB+\angle AOB+\angle AOB_{1}=15^{\circ}+15^{\circ}+15^{\circ}=45^{\circ}.
Следовательно, при пересечении прямых a_{1}
и b_{1}
образуются углы, равные 45^{\circ}
, 45^{\circ}
, 135^{\circ}
, 135^{\circ}
.