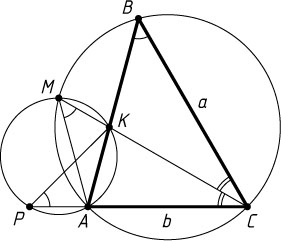
2735. В треугольнике ABC
стороны CB
и CA
равны соответственно a
и b
. Биссектриса угла ACB
пересекает сторону AB
в точке K
, а описанную около треугольника ABC
окружность — в точке M
. Окружность, описанная около треугольника AMK
, вторично пересекает прямую CA
в точке P
. Найдите AP
.
Ответ. |a-b|
.
Указание. \angle APK=\angle AMC=\angle CBA
; треугольники CKP
и CKB
равны.
Решение. Предположим, что a\gt b
. Рассмотрим окружность, описанную около треугольника AMK
. APK
и AMK
— вписанные углы, опирающиеся на одну дугу, поэтому \angle APK=\angle AMC
, а так как ABC
и AMC
— вписанные углы окружности, описанной около треугольника ABC
, то
\angle KBC=\angle ABC=\angle AMC=\angle AMK=\angle APK.
Тогда
\angle BKC=180^{\circ}-\angle KBC-\angle BCK=180^{\circ}-\angle APK-\angle PCK=\angle PKC,
значит, треугольники BKC
и PKC
равны по стороне и двум прилежащим к ней углам. Поэтому CP=BC=a
. Следовательно,
AP=CP-AC=a-b.
Если a\lt b
, то аналогично получим, что AP=b-a
.
Источник: Соросовская олимпиада. — 1996-97, III, 2-й тур, 9 класс
