2750. В квадрат, площадь которого равна 18, вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Стороны прямоугольника относятся как 1:2
. Найдите площадь прямоугольника.
Ответ. 8.
Указание. Пусть стороны прямоугольника равны x
и 2x
, а один из углов (с вершиной на стороне квадрата) между стороной прямоугольника и стороной квадрата равен \alpha
. Выразите соседние стороны квадрата через x
и \alpha
. Докажите, что \alpha=45^{\circ}
.
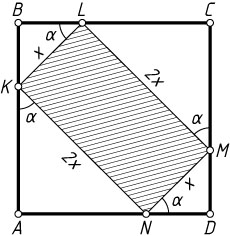
Решение. Пусть вершины K
, L
, M
и N
прямоугольника KLMN
расположены соответственно на сторонах AB
, BC
, CD
и AD
квадрата ABCD
, причём KN=2KL
. Обозначим KL=x
, \angle AKN=\alpha
. Тогда
MN=x,~LM=KN=2x,~\angle CML=\angle BLK=\angle AKN=\alpha.
Из прямоугольных треугольников AKN
, BKL
и CML
находим, что
AK=KN\cos\alpha=2x\cos\alpha,~BK=KL\sin\alpha=x\sin\alpha,
BL=KL\cos\alpha=x\cos\alpha,~CL=LM\sin\alpha=2x\sin\alpha.
Поскольку AB=AK+BK
и BC=BL+CL
, то
2x\cos\alpha+x\sin\alpha=x\cos\alpha+2x\sin\alpha,
откуда находим, что \sin\alpha=\cos\alpha
, а так как \alpha\lt90^{\circ}
, то \alpha=45^{\circ}
.
Поскольку 2x\cos\alpha+x\sin\alpha=AB=\sqrt{18}=3\sqrt{2}
, то
2x\cdot\frac{\sqrt{2}}{2}+x\cdot\frac{\sqrt{2}}{2}=3\sqrt{2},
откуда находим, что MN=KL=x=2
. Тогда LM=KN=2x=4
. Следовательно, S_{KLMN}=KL\cdot KN=8
.
Источник: Вступительный экзамен на химический факультет МГУ. — 1993, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 602
