2752. Через точку пересечения диагоналей трапеции проведена прямая, параллельная основанию и пересекающая боковые стороны в точках E
и F
. Отрезок EF
равен 2. Найдите основания, если их отношение равно 4.
Ответ. 5, \frac{5}{4}
.
Указание. Пусть O
— точка пересечения диагоналей трапеции. Рассмотрите пары подобных треугольников и выразите OE
и OF
через основания трапеции.
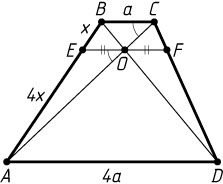
Решение. Пусть диагонали AC
и BD
трапеции ABCD
с основаниями BC
и AD=4BC
пересекаются в точке O
, а прямая, проходящая через точку O
параллельно основаниям, пересекает боковые стороны AB
и CD
в точках E
и F
соответственно.
Из подобия треугольников BOC
и DOA
находим, что
\frac{AO}{OC}=\frac{AD}{BC}=4.
Поэтому \frac{AO}{AC}=\frac{4}{5}
.
Из подобия треугольников AOE
и ACB
находим, что
OE=BC\cdot\frac{AO}{AC}=\frac{4}{5}BC.
Аналогично OF=\frac{4}{5}BC
. Значит,
EF=OE+OF=\frac{8}{5}BC=2,
откуда
BC=\frac{5}{4},~AD=5.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1993, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 607
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.29.1, с. 61
