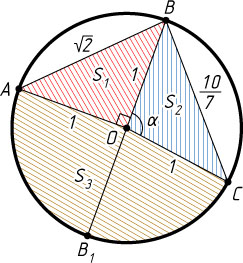
2757. В круге радиуса 1 проведены хорды AB=\sqrt{2}
и BC=\frac{10}{7}
. Найдите площадь части круга, лежащей внутри угла ABC
, если угол BAC
острый.
Ответ. \frac{1}{2}+\frac{10\sqrt{6}}{49}+\frac{3\pi}{4}-\arcsin\frac{5}{7}
.
Указание. Пусть O
— центр окружности. Докажите, что точки A
и C
лежат по разные стороны от прямой OA
. Искомая площадь равна сумме площадей треугольников AOB
, BOC
и сектора AOC
, не содержащего точку B
.
Решение. Докажем сначала, что точки A
и C
лежат по разные стороны от диаметра BB_{1}
. Предположим, что это не так. Тогда треугольник ABC
— тупоугольный, угол ABC
— острый, значит, один из оставшихся двух углов треугольника ABC
— тупой. Так как
BC=\frac{10}{7}\gt\sqrt{2}=AB,
то \angle BAC\gt\angle ACB
, поэтому угол BAC
— тупой, что противоречит условию.
Треугольник AOB
прямоугольный, так как его стороны равны 1, 1 и \sqrt{2}
. Обозначим \angle BOC=\alpha
. Тогда
\sin\frac{\alpha}{2}=\frac{BC}{2OB}=\frac{5}{7}.
Поэтому
\sin\alpha=2\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}=2\cdot\frac{5}{7}\cdot\frac{2\sqrt{6}}{7}=\frac{20\sqrt{6}}{49},
\angle AOC=2\pi-\frac{\pi}{2}-2\arcsin\frac{5}{7}.
Пусть O
— центр окружности. Обозначим искомую площадь через S
, площади треугольников AOB
и AOC
— через S_{1}
и S_{2}
соответственно, площадь сектора AOC
, содержащего точку B_{1}
, — через S_{3}
. Тогда
S_{1}=\frac{1}{2}OA\cdot OB=\frac{1}{2},~S_{2}=\frac{1}{2}OB\cdot OC\sin\alpha=\frac{10\sqrt{6}}{49},
S_{3}=\frac{\pi\angle AOC}{2\pi}=\frac{1}{2}\left(2\pi-\frac{\pi}{2}-2\arcsin\frac{5}{7}\right)=\frac{3\pi}{4}-\arcsin\frac{5}{7}.
Следовательно,
S=S_{1}+S_{2}+S_{3}=\frac{1}{2}+\frac{10\sqrt{6}}{49}+\frac{3\pi}{4}-\arcsin\frac{5}{7}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1994 (предварительный экзамен), № 3, вариант 1
