2759. Отрезки, соединяющие основания высот остроугольного треугольника, равны 5, 12 и 13. Найдите радиус описанной около треугольника окружности.
Ответ. 13.
Решение. Пусть продолжения высот AA_{1}
, BB_{1}
и CC_{1}
треугольника ABC
пересекают описанную окружность в точках A_{2}
, B_{2}
и C_{2}
соответственно, а H
— точка пересечения высот. Тогда A_{1}
, B_{1}
и C_{1}
— середины отрезков HA_{2}
, HB_{2}
и HC_{2}
, поэтому A_{1}B_{1}
, A_{1}C_{1}
и B_{1}C_{1}
— средние линии треугольников A_{2}HB_{2}
, A_{2}HC_{2}
и B_{2}HC_{2}
. Значит, треугольник A_{2}B_{2}C_{2}
подобен треугольнику A_{1}B_{1}C_{1}
, а так как треугольник A_{1}B_{1}C_{1}
— прямоугольный (5^{2}+12^{2}=13^{2}
), то треугольник A_{2}B_{2}C_{2}
— также прямоугольный, причём его угол, лежащий против наибольшей стороны A_{2}B_{2}
, равен 90^{\circ}
. Следовательно, диаметр описанной окружности треугольника A_{2}B_{2}C_{2}
, а значит, и треугольника ABC
, равен гипотенузе треугольника A_{2}B_{2}C_{2}
, т. е. 26, а искомый радиус равен 13.
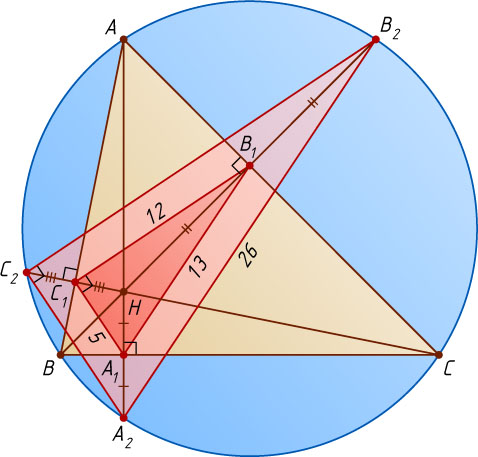
Источник: Вступительный экзамен на экономический факультет МГУ. — 1993, № 5, вариант 4
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.17, с. 123
