2762. В трапеции ABCD
с основаниями AD
и BC
диагонали AC
и BD
пересекаются в точке E
. Вокруг треугольника ECB
описана окружность, а касательная к этой окружности, проведённая в точке E
, пересекает прямую AD
в точке F
таким образом, что точки A
, D
и F
лежат последовательно на этой прямой. Известно, что AF=a
, AD=b
. Найдите EF
.
Ответ. \sqrt{a(a-b)}
.
Указание. Докажите подобие треугольников DEF
и EAF
.
Решение. Угол, вертикальный с углом DEF
, равен половине дуги BE
, не содержащей точки C
(как угол между касательной и хордой), поэтому
\angle CAD=\angle BCE=\angle DEF.
Значит, треугольники DEF
и EAF
подобны по двум углам (угол при вершине F
— общий). Поэтому \frac{DF}{EF}=\frac{EF}{AF}
, откуда находим, что
EF^{2}=DF\cdot AF=a(a-b).
Следовательно, EF=\sqrt{a(a-b)}
.
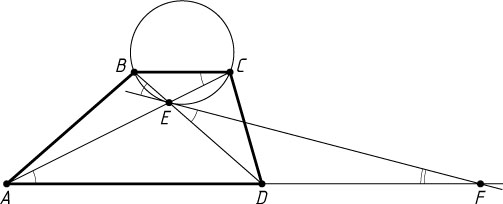
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1994 (основной экзамен), вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 594
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.30, с. 113
