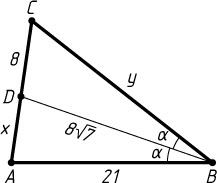
2764. В треугольнике ABC
сторона AB
равна 21, биссектриса BD
равна 8\sqrt{7}
, а DC=8
. Найдите периметр треугольника ABC
.
Ответ. 60.
Указание. Примените свойство биссектрисы треугольника и теоремы синусов и косинусов.
Решение. Обозначим AD=x
, BC=y
, \angle ABD=\angle CBD=\alpha
.
По свойству биссектрисы треугольника \frac{AB}{BC}=\frac{AD}{DC}
, или \frac{21}{y}=\frac{x}{8}
, откуда находим, что y=\frac{21\cdot8}{x}
. По теореме синусов для треугольников ABC
и DBC
имеем:
\frac{AC}{\sin\angle ABC}=\frac{AB}{\sin\angle C},~\frac{DC}{\sin\angle CBD}=\frac{BD}{\sin\angle C},
или
\frac{x+8}{\sin2\alpha}=\frac{21}{\sin\angle C},~\frac{8}{\sin\alpha}=\frac{8\sqrt{7}}{\sin\angle C}.
Разделив почленно первое уравнение на второе и применив формулу \sin2\alpha=2\sin\alpha\cos\alpha
, получим, что
\frac{x+8}{2\cos\alpha}=\frac{21}{\sqrt{7}},
откуда \cos\alpha=\frac{x+8}{6\sqrt{7}}
.
По теореме косинусов из треугольника ABD
находим, что
x^{2}=21^{2}+(8\sqrt{7})^{2}-2\cdot21\cdot8\sqrt{7}\cdot\frac{x+8}{6\sqrt{7}},
или
x^{2}+56x-441=0,
откуда x=7
. Тогда y=\frac{21\cdot8}{x}=24
. Следовательно, периметр треугольника ABC
равен
AB+AC+BC=AB+(AD+CD)+BC=21+7+8+24=60.
