2773. В трапеции ABCD
даны основания AD=4
, BC=1
и углы A
и D
при основании, равные соответственно \arctg2
и \arctg3
. Найдите радиус окружности, вписанной в треугольник CBE
, где E
— точка пересечения диагоналей трапеции.
Ответ. \frac{18}{25+2\sqrt{130}+\sqrt{445}}
.
Указание. Радиус вписанной окружности треугольника равен его площади, делённой на полупериметр.
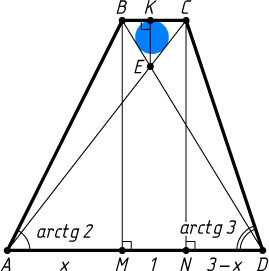
Решение. Опустим перпендикуляры BM
и CN
на основание AD
трапеции ABCD
. Обозначим AM=x
. Тогда
DN=AD-MN-AM=4-1-x=3-x.
Из прямоугольных треугольников ABM
и DCN
находим, что
BM=AM\tg\angle BAM=2x,~CN=DN\tg\angle CDN=3(3-x),
а так как BM=CN
, то 2x=3(3-x)
, откуда x=\frac{9}{5}
. Значит,
AN=AM+MN=\frac{9}{5}+1=\frac{14}{5},
DM=MN+DN=1+3-\frac{9}{5}=\frac{11}{5}.
По теореме Пифагора из прямоугольных треугольников ACN
и DBM
находим, что
AC=\sqrt{AN^{2}+CN^{2}}=\sqrt{\left(\frac{14}{5}\right)^{2}+\left(\frac{18}{5}\right)^{2}}=\frac{2\sqrt{130}}{5},
BD=\sqrt{DM^{2}+BM^{2}}=\sqrt{\left(\frac{11}{5}\right)^{2}+\left(\frac{18}{5}\right)^{2}}=\frac{\sqrt{445}}{5}.
Пусть EK
— высота треугольника BEC
. Поскольку треугольник BEC
подобен треугольнику DEA
с коэффициентом \frac{BC}{AD}=\frac{1}{4}
, то
EK=\frac{1}{5}BM=\frac{18}{25},~CE=\frac{1}{5}AC=\frac{2\sqrt{130}}{25},~BE=\frac{1}{5}BD=\frac{\sqrt{445}}{25}.
Тогда
S_{\triangle BEC}=\frac{1}{2}BC\cdot EK=\frac{9}{25}.
Радиус r
вписанной окружности треугольника равен его площади, делённой на полупериметр, следовательно,
r=\frac{\frac{9}{25}}{\frac{1}{2}+\frac{\sqrt{130}}{25}+\frac{\sqrt{445}}{50}}=\frac{18}{25+2\sqrt{130}+\sqrt{445}}.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1994, № 4, вариант 1
