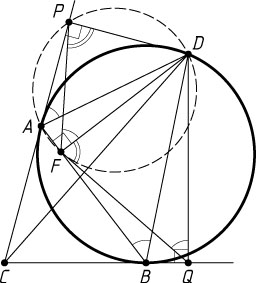
2775. Через точку C
проведены две прямые, касающиеся заданной окружности в точках A
и B
. На большей из дуг AB
взята точка D
, для которой CD=2
и \sin\angle ACD\cdot\sin\angle BCD=\frac{1}{3}
. Найдите расстояние от точки D
до хорды AB
.
Ответ. \frac{2\sqrt{3}}{3}
.
Указание. Опустите перпендикуляры DP
, DF
и DQ
из точки D
на прямые AC
, AB
и BC
соответственно и докажите подобие треугольников FPD
и QFD
.
Решение. Пусть P
, F
и Q
— основания перпендикуляров, опущенных из точки D
на прямые AC
, AB
и BC
соответственно. Поскольку отрезок AD
виден из точек P
и F
под прямым углом, то эти точки лежат на окружности с диаметром AD
. Аналогично докажем, что точки Q
и F
лежат на окружности с диаметром BD
. Поэтому
\angle DFP=\angle DAP=\angle ABD=\angle DQF.
Аналогично докажем, что \angle DPF=\angle DFQ
. Значит треугольники FPD
и QFD
подобны по двум углам. Следовательно,
\frac{DP}{DF}=\frac{DF}{DQ},
DF^{2}=DP\cdot DQ=(CD\sin\angle ACD)\cdot(CD\sin\angle BCD)=\frac{1}{3}CD^{2}=\frac{4}{3}.
Следовательно,
DF=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1994 (предварительный экзамен), № 5, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.19, с. 112
