2779. В треугольнике KMN
проведены высота NA
, биссектриса NB
и медиана NC
, которые делят угол KNM
на четыре равные части. Найдите длины высоты NA
, биссектрисы NB
и медианы NC
, если радиус описанной около треугольника KMN
окружности равен R
.
Ответ. \frac{R\sqrt{2}}{2}
, R\sqrt{2-\sqrt{2}}
, R
.
Указание. Докажите, что треугольник KMN
— прямоугольный. Для этого продолжите NA
, NB
и NC
до пересечения с описанной окружностью треугольника KMN
.
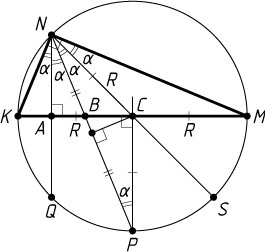
Решение. Пусть лучи NA
, NB
и NC
пересекают описанную окружность треугольника KMN
в точках Q
, P
и S
соответственно. Обозначим
\angle KNQ=\angle QNP=\angle PNS=\angle MNS=\alpha.
Из равенства дуг KQ
и MS
, не содержащих точку N
, следует параллельность хорд QS
и KM
, поэтому
\angle NQS=\angle NAM=90^{\circ}.
Поскольку P
— середина дуги KQM
, то PC
— серединный перпендикуляр к стороне KM
треугольника KMN
, а так как P
— середина дуги QS
, то PC
— серединный перпендикуляр к стороне QS
прямоугольного треугольника NQS
. Значит, C
— центр окружности, описанной около прямоугольного треугольника NQS
. Таким образом, центр описанной окружности треугольника KNM
лежит на стороне KM
, поэтому треугольник KNM
прямоугольный, а KM=2R
— его гипотенуза.
Из уравнения 4\alpha=90^{\circ}
находим, что \alpha=22{,}5^{\circ}
. Следовательно,
\angle NKM=90^{\circ}-\alpha=67{,}5^{\circ},~\angle KMN=\alpha=22{,}5^{\circ},
NC=R,~KN=KM\sin\angle KMN=2R\cdot\sin\alpha,
NA=KN\cos\angle ANK=2R\sin\alpha\cos\alpha=R\sin2\alpha=R\sin45^{\circ}=\frac{R\sqrt{2}}{2},
NB=\frac{NA}{\cos\angle ANB}=\frac{NA}{\cos\alpha}=R\sqrt{2-\sqrt{2}}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1994 (предварительный экзамен), № 5, вариант 1
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 5.32, с. 50
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.33.1, с. 52
