2781. Вне прямоугольного треугольника ABC
на его катетах AC
и BC
построены квадраты ACDE
и BCFG
. Продолжение высоты CH
треугольника ABC
пересекает прямую DF
в точке K
. Найдите HK
, если катеты равны 2 и 3.
Ответ. \frac{25}{2\sqrt{13}}
.
Указание. Докажите, что CK
— медиана прямоугольного треугольника CDF
.
Решение. Пусть AC=3
, BC=2
. Обозначим \angle BAC=\alpha
. Прямоугольные треугольники ABC
и DFC
равны по двум катетам, поэтому
DF=AB=\sqrt{AB^{2}+BC^{2}}=\sqrt{13},
\angle CDF=\angle BAC=\alpha,~\angle DCK=\angle BCH=\angle BAC=\alpha,
значит, треугольник DKC
равнобедренный, CK=DK
. Аналогично докажем, что CK=FK
. Следовательно,
CK=\frac{1}{2}DF=\frac{\sqrt{13}}{2}.
Поскольку AC\cdot BC=AB\cdot CH
(удвоенная площадь треугольника ABC
), то
CH=AC\cdot\frac{BC}{AB}=\frac{6}{\sqrt{13}}.
Следовательно,
HK=CH+CK=\frac{6}{\sqrt{13}}+\frac{\sqrt{13}}{2}=\frac{25}{2\sqrt{13}}.
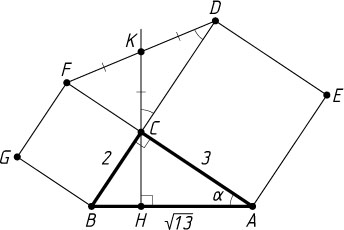
Источник: Вступительный экзамен на географический факультет МГУ. — 1994, основной экзамен, № 4, вариант 2
