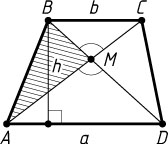
2798. В трапеции ABCD
(BC\parallel AD
) диагонали пересекаются в точке M
, BC=b
, AD=a
. Найдите отношение площади треугольника ABM
к площади трапеции ABCD
.
Ответ. \frac{ab}{(a+b)^{2}}
.
Указание. S_{\triangle ABM}=\frac{BM}{BD}\cdot S_{\triangle ABD}
, \frac{S_{\triangle ABD}}{S_{ABCD}}=\frac{a}{a+b}
.
Решение. Из подобия треугольников BMC
и DMA
следует, что
\frac{BM}{MD}=\frac{BC}{AD}=\frac{b}{a},
поэтому
\frac{BM}{BD}=\frac{b}{a+b},~S_{\triangle ABM}=\frac{BM}{BD}\cdot S_{\triangle ABD}=\frac{b}{a+b}\cdot S_{\triangle ABD}.
Пусть h
— высота трапеции. Тогда
S_{ABCD}=\frac{a+b}{2}\cdot h,~S_{\triangle ABD}=\frac{1}{2}ah,~\frac{S_{\triangle ABD}}{S_{ABCD}}=\frac{a}{a+b}.
Следовательно,
\frac{S_{\triangle ABM}}{S_{ABCD}}=\frac{b}{a+b}\cdot\frac{S_{\triangle ABD}}{S_{ABCD}}=\frac{b}{a+b}\cdot\frac{a}{a+b}=\frac{ab}{(a+b)^{2}}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1995 (предварительный экзамен, май), № 6, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.17, с. 53
