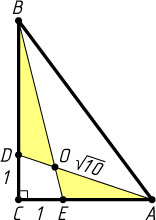
2803. В прямоугольном треугольнике ABC
точки D
и E
лежат соответственно на катетах BC
и AC
, причём CD=CE=1
. Точка O
есть точка пересечения отрезков AD
и BE
. Площадь треугольника BOD
больше площади треугольника AOE
на \frac{1}{2}
. Кроме того, известно, что AD=\sqrt{10}
. Найдите гипотенузу AB
.
Ответ. 5.
Указание. Площадь треугольника BCE
также на \frac{1}{2}
больше площади треугольника ACD
.
Решение. По теореме Пифагора из прямоугольного треугольника ACD
находим, что
AC=\sqrt{AD^{2}-CD^{2}}=\sqrt{10-1}=3,
поэтому
AE=AC-CE=3-1=2,
значит,
S_{\triangle ACD}=\frac{1}{2}AC\cdot DC=\frac{3}{2},
а так как площадь треугольника BOD
на \frac{1}{2}
больше площади треугольника AOE
, то площадь треугольника BCE
также на \frac{1}{2}
больше площади треугольника ACD
, т. е.
S_{\triangle BCE}=S_{\triangle ACD}+\frac{1}{2}=\frac{3}{2}+\frac{1}{2}=2.
Из равенства \frac{1}{2}CE\cdot BC=2
, находим, что BC=\frac{4}{CE}=4
. Следовательно,
AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{9+16}=5.
Источник: Вступительный экзамен на химический факультет МГУ. — 1995 (предварительный экзамен), № 4, вариант 1
