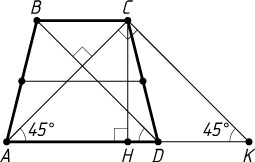
2805. Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если её средняя линия равна 5.
Ответ. 25.
Указание. Пусть CH
— перпендикуляр, опущенный из вершины C
меньшего основания BC
данной трапеции ABCD
, на большее основание AD
. Тогда
AH=\frac{AD+BC}{2}.
Решение. Первый способ. Пусть CH
— перпендикуляр, опущенный из вершины C
меньшего основания BC
данной трапеции ABCD
, на большее основание AD
. Тогда
AH=\frac{AD+BC}{2}=5,
а так как \angle CAD=\angle BDA=45^{\circ}
, то CH=AH=5
. Следовательно,
S_{ABCD}=\frac{AD+BC}{2}\cdot CH=AH\cdot CH=25.
Второй способ. Через вершину C
меньшего основания BC
данной трапеции ABCD
проведём прямую, параллельную диагонали BD
, до пересечения с продолжением основания AD
в точке K
. Тогда
DK=BC,~\angle ACK=90^{\circ},~CK=BD=AC,~\angle CKA=\angle CAK=45^{\circ},
AK=AD+DK=AD+BC.
Пусть h
— высота трапеции. Тогда
h=\frac{1}{2}AK,~S_{ABCD}=\frac{AD+BC}{2}\cdot h=\frac{1}{2}AK\cdot h=\frac{1}{4}AK^{2}=\frac{1}{4}\cdot100=25.
Источник: Вступительный экзамен на химический факультет МГУ. — 1995 (основной экзамен), № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.4, с. 30
