2817. В треугольнике ABC
известны высоты: h_{a}=\frac{1}{3}
, h_{b}=\frac{1}{4}
, h_{c}=\frac{1}{5}
. Найдите отношение биссектрисы CD
к радиусу описанной окружности.
Ответ. \frac{24\sqrt{2}}{35}
.
Указание. Произведение стороны треугольника на проведённую к ней высоту для данного треугольника постоянно.
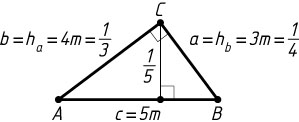
Решение. Обозначим BC=a
, AC=b
, AB=c
(рис. 1). Поскольку площадь треугольника равна половине произведения стороны на проведённую к ней высоту, то
a\cdot\frac{1}{3}=b\cdot\frac{1}{4}=c\cdot\frac{1}{5},
откуда b=\frac{4a}{3}
и c=\frac{5a}{3}
. Обозначив \frac{1}{3}a=m
, получим:
a=3m,~b=4m,~c=5m.
Треугольник ABC
прямоугольный, так как
a^{2}+b^{2}=9m^{2}+16m^{2}=25m^{2}=c^{2}.
Радиус R
его описанной окружности равен половине гипотенузы, т. е.
R=\frac{c}{2}=\frac{5m}{2}.
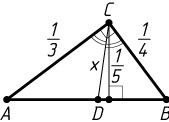
Обозначим CD=x
(рис. 2). Тогда
S_{\triangle ABC}=\frac{1}{2}ab,~S_{\triangle BCD}=\frac{1}{2}ax\sin45^{\circ}=\frac{ax\sqrt{2}}{4},~S_{\triangle ACD}=\frac{1}{2}bx\sin45^{\circ}=\frac{bx\sqrt{2}}{4},
а так как S_{\triangle BCD}+S_{\triangle ACD}=S_{\triangle ABC}
, имеем уравнение
x(a+b)\sqrt{2}=2ab,
откуда находим, что
x=\frac{ab\sqrt{2}}{a+b}=\frac{12m\sqrt{2}}{7}.
Следовательно,
\frac{CD}{R}=\frac{\frac{12m\sqrt{2}}{7}}{\frac{5m}{2}}=\frac{24\sqrt{2}}{35}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1995 (предварительный экзамен), № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.32.1, с. 52

