2820. Биссектриса одного из острых углов прямоугольного треугольника в точке пересечения с высотой, опущенной на гипотенузу, делится на отрезки, отношение которых равно 1+\sqrt{2}
, считая от вершины. Найдите острые углы треугольника.
Ответ. 45^{\circ}
, 45^{\circ}
.
Указание. Рассмотрите подобные треугольники.
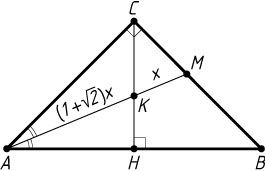
Решение. Пусть биссектриса AM
прямоугольного треугольника ABC
и высота CH
, проведённая из вершины прямого угла, пересекаются в точке K
, причём \frac{AK}{KM}=1+\sqrt{2}
. Прямоугольные треугольники AHK
и ACM
подобны, так как равны их острые углы HAK
и CAM
. Поэтому
\cos\angle CAH=\frac{AH}{AC}=\frac{AK}{AM}=\frac{1+\sqrt{2}}{(1+\sqrt{2})+1}=\frac{1+\sqrt{2}}{2+\sqrt{2}}=\frac{1+\sqrt{2}}{\sqrt{2}(\sqrt{2}+1)}=\frac{1}{\sqrt{2}}.
Следовательно,
\angle CAB=\angle CAH=45^{\circ}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1995, № 6, вариант 1
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14.37, с. 139
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 14.37.1, с. 150
