2826. В трапеции ABCD
известны боковые стороны AB=27
, CD=28
, основание BC=5
и \cos\angle BCD=-\frac{2}{7}
. Найдите диагональ AC
.
Ответ. 28
, 2\sqrt{181}
.
Решение. Поскольку \cos\angle BCD=-\frac{2}{7}\lt0
, угол BCD
— тупой, поэтому угол ADC
— острый и \cos\angle ADC=\frac{2}{7}
. Опустим перпендикуляр CH
на основание AD
. Тогда
DH=CD\cos\angle ADC=28\cdot\frac{2}{7}=8,
CH=CD\sin\angle ADC=28\sqrt{1-\frac{4}{49}}=12\sqrt{5}.
Через вершину C
проведём прямую, параллельную боковой стороне AB
, до пересечения с прямой AD
в точке P
. Тогда
PH=\sqrt{CP^{2}-CH^{2}}=\sqrt{AB^{2}-CH^{2}}=\sqrt{27^{2}-(12\sqrt{5})^{2}}=3.
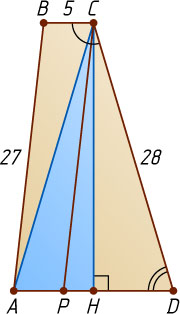
Если точка P
лежит между A
и H
(рис. 1), то
AH=AP+PH=5+3=8.
В этом случае
AC=\sqrt{AH^{2}+CH^{2}}=\sqrt{64+144\cdot5}=28.
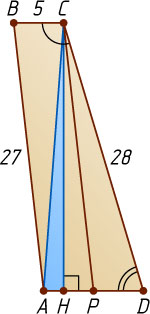
Если точка P
лежит между D
и H
(рис. 2), то
AH=AP-PH=5-3=2.
В этом случае
AC=\sqrt{AH^{2}+CH^{2}}=\sqrt{4+144\cdot5}=2\sqrt{181}.
Источник: Вступительный экзамен на экономический факультет МГУ. — (отделение экономики) 1995, № 3, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.28, с. 32

