2829. В треугольнике ABC
проведены биссектрисы BL
и AE
, которые пересекаются в точке O
. Известно, что AB=BL
, периметр треугольника ABC
равен 28, BO=2OL
. Найдите AB
.
Ответ. 8.
Указание. Воспользуйтесь свойством биссектрисы треугольника и теоремой косинусов.
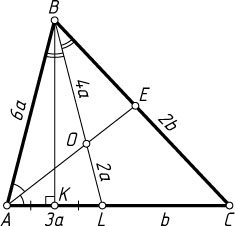
Решение. Пусть OL=2a
, BO=4a
. Тогда AB=BL=6a
. Поскольку AO
— биссектриса треугольника ABL
, то \frac{AB}{AL}=\frac{BO}{OL}=2
, поэтому AL=\frac{1}{2}AB=3a
.
Пусть CL=b
. Поскольку BL
— биссектриса треугольника ABC
, то \frac{BC}{CL}=\frac{AB}{AL}=2
, поэтому BC=2CL=2b
.
Высота BK
равнобедренного треугольника ABL
делит пополам основание AL
, поэтому \cos\angle BAC=\frac{AK}{AB}=\frac{1}{4}
. По теореме косинусов
BC^{2}=AB^{2}+AC^{2}-2AB\cdot AC\cos\angle BAC,~\mbox{или}
4b^{2}=36a^{2}+(3a+b)^{2}-3a(3a+b).
После очевидных преобразований получим уравнение
b^{2}-ab-12a^{2}=0,
откуда находим, что b=4a
. Тогда периметр треугольника ABC
равен
AB+BC+AC=6a+8a+7a=21a=28,
откуда a=\frac{4}{3}
. Следовательно, AB=6a=8
.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1995, № 4, вариант 1
