2843. Через центр O
вписанной в треугольник ABC
окружности проведена прямая, параллельная стороне BC
и пересекающая стороны AB
и AC
соответственно в точках M
и N
. Площадь треугольника ABC
равна \sqrt{15}
, отрезок BC
равен 2, а отрезок AO
в четыре раза больше радиуса вписанной в треугольник ABC
окружности. Найдите периметр треугольника AMN
.
Ответ. 8.
Указание. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. Периметр треугольника AMN
равен AB+AC
.
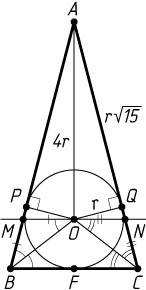
Решение. Пусть окружность радиуса r
, вписанная в треугольник ABC
, касается его сторон AB
, BC
и AC
в точках P
, F
и Q
соответственно. Тогда
AP=AQ=\sqrt{AO^{2}-OQ^{2}}=\sqrt{16r^{2}-r^{2}}=r\sqrt{15},
а периметр треугольника ABC
равен
AB+AC+BC=AP+PB+AQ+QC+BC=
=AP+AQ+(PB+QC)+BC=AP+AQ+(BF+CF)+BC=
=2AP+2BC=2r\sqrt{15}+4.
Площадь треугольника ABC
равна произведению его полупериметра на радиус вписанной окружности, поэтому
\sqrt{15}=(r\sqrt{15}+2)r,
откуда r=\frac{3}{\sqrt{15}}
. Следовательно, AP=AQ=r\sqrt{15}=3
.
Поскольку BO
— биссектриса угла ABC
и MN\parallel BC
, то
\angle MOB=\angle OBC=\angle OBM,
значит, OM=MB
. Аналогично докажем, что ON=NC
. Поэтому периметр треугольника AMN
равен
AM+MN+AN=(AM+OM)+(ON+AN)=
=(AM+MB)+(AN+NC)=AB+AC=
=AP+PB+AQ+QC=(AP+AQ)+(BF+CF)=
=2AP+BC=2\cdot3+2=8.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1996 (предварительный экзамен), № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8.37, с. 77
