2853. Площадь равнобедренной трапеции равна \sqrt{3}
. Угол между диагональю и основанием на 20^{\circ}
больше угла между диагональю и боковой стороной. Найдите острый угол трапеции, если её диагональ равна 2.
Ответ. 40^{\circ}
или 80^{\circ}
.
Указание. Высота равнобедренной трапеции, опущенная из вершины меньшего основания, делит большее основание на отрезки, один из которых равен полуразности оснований, а другой — полусумме.
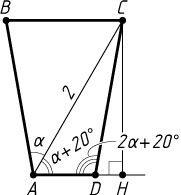
Решение. Пусть AD
— большее основание равнобедренной трапеции ABCD
. Тогда угол BAD
— острый. Если CH
— высота трапеции, то
DH=\frac{AD-BC}{2},~AH=AD-DH=AD-\frac{AD-BC}{2}=\frac{AD+BC}{2},
поэтому
S_{ABCD}=\frac{AD+BC}{2}\cdot CH=AH\cdot CH=\sqrt{3}.
Обозначим \angle BAC=\alpha
. Тогда \angle CAH=\alpha+20^{\circ}
. Из прямоугольного треугольника AHC
находим, что
AH=AC\cos\angle CAH=2\cos(\alpha+20^{\circ}),
CH=AC\sin\angle CAH=2\sin(\alpha+20^{\circ}),
поэтому
AH\cdot CH=2\cos(\alpha+20^{\circ})\cdot2\sin(\alpha+20^{\circ})=2\sin(2\alpha+40^{\circ})=\sqrt{3}.
Значит, 2\alpha+40^{\circ}=60^{\circ}
или 2\alpha+40^{\circ}=120^{\circ}
. Отсюда находим, что \alpha=10^{\circ}
или \alpha=40^{\circ}
, а \angle BAD=2\alpha+20^{\circ}=40^{\circ}
или \angle BAD=100^{\circ}
. Поскольку угол BAD
— острый, подходит только 40^{\circ}
.
Если AD
— меньшее основание, то аналогично находим, что \angle ABC=80^{\circ}
.

Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.23, с. 31

