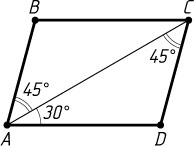
2855. Диагональ параллелограмма делит его угол на части в 30^{\circ}
и 45^{\circ}
. Найдите отношение сторон параллелограмма.
Ответ. \sqrt{2}
.
Указание. Примените теорему синусов (или опустите перпендикуляры из вершин B
и D
на диагональ AC
).
Решение. Первый способ. Пусть диагональ AC
параллелограмма ABCD
делит угол при вершине A
на два угла: \angle BAC=45^{\circ}
и \angle DAC=30^{\circ}
. Тогда
\angle ACB=\angle DAC=30^{\circ}.
Применяя теорему синусов к треугольнику ABC
, найдём, что
\frac{BC}{AB}=\frac{\sin\angle BAC}{\sin\angle ACB}=\frac{\sin45^{\circ}}{\sin30^{\circ}}=\sqrt{2}.
Второй способ. Пусть \angle DAC=30^{\circ}
, \angle BAC=45^{\circ}
. Опустим перпендикуляры DQ
и BP
из вершин D
и B
на диагональ AC
. Тогда BP=DQ
как высоты равных треугольников ABC
и CDA
. Из прямоугольных треугольников ABP
и ADQ
находим, что
AB=\frac{BP}{\sin\angle BAC}=\frac{BP}{\sin45^{\circ}}=BP\sqrt{2},
AD=\frac{DQ}{\sin\angle DAC}=\frac{DQ}{\sin30^{\circ}}=2DQ.
Следовательно,
\frac{AD}{AB}=\frac{2DQ}{BP\sqrt{2}}=\sqrt{2}.
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 231, с. 37
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.2, с. 23
