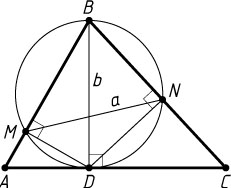
2862. В остроугольном треугольнике ABC
из основания D
высоты BD
опущены перпендикуляры DM
и DN
на стороны AB
и BC
. Известно, что MN=a
, BD=b
. Найдите угол ABC
.
Ответ. \arcsin\frac{a}{b}
.
Указание. Точки M
и N
лежат на окружности с диаметром BD
.
Решение. Поскольку \angle BMD=\angle BND=90^{\circ}
, то отрезок BD
виден из точек M
и N
под прямым углом, поэтому точки M
и N
лежат на окружности с диаметром BD=2R
, где R
— радиус этой окружности. Значит,
MN=2R\sin\angle ABC.
Следовательно,
\sin\angle ABC=\frac{MN}{2R}=\frac{MN}{BD}=\frac{a}{b}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.18, с. 104
