2864. В окружности радиуса R
проведены хорда AB
и диаметр AC
. Хорда PQ
, перпендикулярная диаметру AC
, пересекает хорду AB
в точке M
. Известно, что AB=a
, PM:MQ=3
. Найдите AM
.
Ответ. \frac{4aR^{2}}{16R^{2}-3a^{2}}
.
Указание. Воспользуйтесь замечательным свойством окружности и теоремой о произведении отрезков пересекающихся хорд.
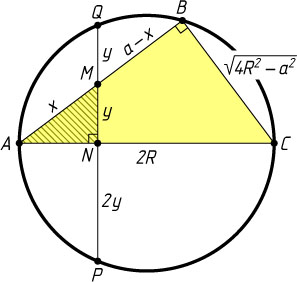
Решение. Пусть диаметр AC
пересекается с хордой PQ
в точке N
. Обозначим AM=x
, PQ=4y
. Тогда BM=AB-AM=a-x
, а так как N
— середина PQ
, то QN=2y
, то MN=QM=y
.
По теореме Пифагора из прямоугольного треугольника ABC
находим, что
BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{4R^{2}-a^{2}}.
Из подобия прямоугольных треугольников ABC
и ANM
находим, что \frac{MN}{AM}=\frac{BC}{AC}
, откуда
y=MN=\frac{AM\cdot BC}{AC}=\frac{x\sqrt{4R^{2}-a^{2}}}{2R}.
По теореме о произведении отрезков пересекающихся хорд
AM\cdot BM=QM\cdot PM,
или
x(a-x)=y\cdot3y=3y^{2}=3\left(\frac{x\sqrt{4R^{2}-a^{2}}}{2R}\right)^{2}=\frac{3}{4}\cdot\frac{x^{2}(4R^{2}-a^{2})}{R^{2}}.
Из уравнения
x(a-x)=\frac{3}{4}\cdot\frac{x^{2}(4R^{2}-a^{2})}{R^{2}}
находим, что
AM=x=\frac{4aR^{2}}{16R^{2}-3a^{2}}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1996 (предварительный экзамен, май), № 6, вариант 1
