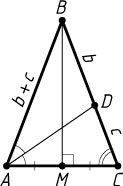
2866. Биссектриса AD
равнобедренного треугольника ABC
(AB=BC
) делит сторону BC
на отрезки BD=b
и DC=c
. Найдите биссектрису AD
.
Ответ. c\sqrt{2+\frac{c}{b}}
.
Указание. Применяя свойство биссектрисы треугольника, найдите AC
, затем найдите \cos\angle BCA
и воспользуйтесь теоремой косинусов.
Решение. Первый способ. По свойству биссектрисы треугольника \frac{AC}{AB}=\frac{CD}{BD}
, откуда находим, что
AC=AB\cdot\frac{CD}{BD}=BC\cdot\frac{CD}{BD}=\frac{(b+c)c}{b}.
Пусть BM
— высота треугольника ABC
. Тогда
CM=\frac{1}{2}AC=\frac{(b+c)c}{2b}.
Из прямоугольного треугольника BMC
находим, что
\cos\angle BCA=\frac{CM}{BC}=\frac{c}{2b}.
По теореме косинусов из треугольника ADC
находим, что
AD^{2}=AC^{2}+CD^{2}-2AC\cdot CD\cos\angle BCA=\frac{(b+c)^{2}c^{2}}{b^{2}}+c^{2}-\frac{2(b+c)c^{2}}{b}\cdot\frac{c}{2b}=
=\frac{c^{2}(b+c)^{2}}{b^{2}}+1-\frac{(b+c)c}{b^{2}}=\frac{c^{2}(2b+c)}{b}=c^{2}\left(2+\frac{c}{b}\right).
Следовательно, AD=c\sqrt{2+\frac{c}{b}}
.
Второй способ. По свойству биссектрисы треугольника \frac{AC}{AB}=\frac{CD}{BD}
, откуда находим, что
AC=AB\cdot\frac{CD}{BD}=BC\cdot\frac{CD}{BD}=\frac{(b+c)c}{b}.
По формуле для квадрата биссектрисы (см. задачу 791)
AD^{2}=AB\cdot AC-BD\cdot CD=(b+c)\cdot\frac{(b+c)c}{b}-bc=c\cdot\frac{(b+c)^{2}-b^{2}}{b}=c^{2}\cdot\frac{2b+c}{b}.
Следовательно, AD=c\sqrt{2+\frac{c}{b}}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.16, с. 40
