2873. Через точку A
, находящуюся вне окружности на расстоянии 7 от её центра, проведена прямая, пересекающая окружность в точках B
и C
. Найдите радиус окружности, если известно, что AB=3
, BC=5
.
Ответ. 5.
Указание. Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
Решение. Поскольку AB\lt BC
, то точка B
лежит между точками A
и C
. Пусть O
— центр окружности, R
— её радиус, а прямая AO
пересекает окружность в точках D
и E
(D
между A
и O
). Тогда
AD\cdot AE=AB\cdot AC,~(7-R)(7+R)=3\cdot8,~49-R^{2}=24,
R^{2}=25
. Следовательно, R=5
.
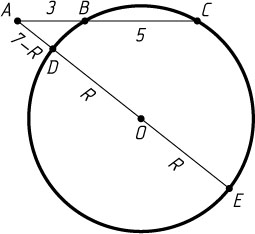
Источник: Вступительный экзамен на экономический факультет МГУ. — 1996 (отделение менеджмента), № 5, вариант 1
