2886. Окружность проходит через вершины A
и C
треугольника ABC
и пересекает сторону AB
в точке D
, а сторону BC
в точке E
. Найдите угол BDC
, если BD:EC=1:2
, BE:AD=2:7
, \angle ABC=60^{\circ}
.
Ответ. \arccos\left(-\frac{1}{\sqrt{13}}\right)
.
Указание. Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
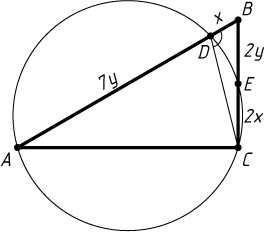
Решение. Положим BD=x
, CE=2x
, BE=2y
, AD=7y
. Поскольку произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно, то
BD\cdot AB=BE\cdot BC,~\mbox{или}~x(x+7y)=2y(2y+2x),~\mbox{или}~x^{2}+3xy-4y^{2}=0.
Из этого уравнения находим, что x=y
.
По теореме косинусов
CD=\sqrt{BD^{2}+BC^{2}-2BD\cdot BC\cos\angle ABC}=\sqrt{x^{2}+16x^{2}-4x^{2}}=x\sqrt{13}.
Следовательно,
\cos\angle BDC=\frac{BD^{2}+CD^{2}-BC^{2}}{2BD\cdot BC}=\frac{x^{2}+13x^{2}-16x^{2}}{2\cdot x\cdot x\sqrt{13}}=-\frac{1}{\sqrt{13}}.
