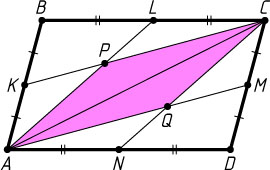
2891. Точки K
, L
, M
и N
— середины сторон соответственно AB
, BC
, CD
и AD
параллелограмма ABCD
площади s
. Найдите площадь четырёхугольника, образованного пересечением прямых AL
, AM
, CK
и CN
.
Ответ. \frac{1}{3}s
.
Решение. Пусть прямые AL
и CK
пересекаются в точке P
, а прямые AM
и CN
— в точке Q
. Тогда P
и Q
— точки пересечения медиан треугольников ABC
и ADC
соответственно. Поэтому
S_{\triangle APC}=\frac{1}{3}S_{\triangle ABC}=\frac{1}{3}\cdot\frac{1}{2}s=\frac{1}{6}s,~S_{\triangle AQC}=\frac{1}{3}S_{\triangle ADC}=\frac{1}{3}\cdot\frac{1}{2}s=\frac{1}{6}s.
Следовательно,
S_{APCQ}=S_{\triangle APC}+S_{\triangle AQC}=\frac{1}{6}s+\frac{1}{6}s=\frac{1}{3}s.