2892. На трёх отрезках OA
, OB
и OC
одинаковой длины (точка B
лежит внутри угла AOC
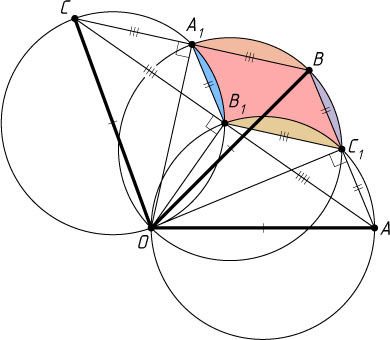
) как на диаметрах построены окружности. Докажите, что площадь криволинейного треугольника, ограниченного дугами этих окружностей и не содержащего точку O
, равна половине площади (обычного) треугольника ABC
.
Решение. Пусть окружности, построенные как на диаметрах на боковых сторонах OA
и OB
равнобедренного треугольника AOB
, пересекаются в точке C_{1}
. Тогда
\angle AC_{1}O=\angle BC_{1}O=90^{\circ},
значит, точка C_{1}
лежит на отрезке AB
. Кроме того, поскольку OC_{1}
— высота равнобедренного треугольника AOB
, точка C_{1}
— середина стороны AB
треугольника ABC
.
Аналогично, точка A_{1}
пересечения окружностей с диаметрами OB
и OC
— середина стороны BC
, а точка B_{1}
пересечения окружностей с диаметрами OA
и OC
— середина стороны AC
. Следовательно, четырёхугольник BA_{1}B_{1}C_{1}
— параллелограмм.
Сегмент окружности с диаметром OB
, отсекаемый хордой BC_{1}
, равен соответствующему сегменту окружности с диаметром OC=OB
, отсекаемому хордой A_{1}B_{1}=BC_{1}
. Аналогично, сегмент окружности с диаметром OB
, отсекаемый хордой BA_{1}
, равен соответствующему сегменту окружности с диаметром OA=OB
, отсекаемому хордой B_{1}C_{1}=BA_{1}
. Следовательно, криволинейный треугольник, о котором говорится в условии задачи, равновелик параллелограмму BA_{1}B_{1}C_{1}
, площадь которого равна половине площади треугольника ABC
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.40
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.41, с. 61
