2902. На сторонах AB
и CD
четырёхугольника ABCD
взяты точки M
и N
так, что AM:MB=CN:ND
. Отрезки AN
и DM
пересекаются в точке K
, а отрезки BN
и CM
— в точке L
. Докажите, что S_{KMLN}=S_{\triangle ADK}+S_{\triangle BCL}
.
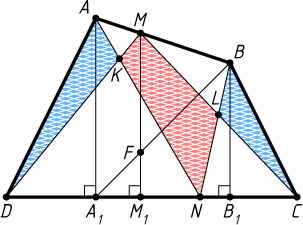
Решение. Пусть A_{1}
, M_{1}
и B_{1}
— проекции точек соответственно A
, M
и B
на прямую CD
, F
— точка пересечения отрезков MM_{1}
и BA_{1}
. Обозначим \frac{AM}{AB}=\frac{CN}{CD}=p
. Тогда
MM_{1}=MF+FM_{1}=AA_{1}\cdot\frac{MB}{AB}+BB_{1}\cdot\frac{A_{1}F}{A_{1}B}=(1-p)AA_{1}+pBB_{1}.
Поэтому
S_{\triangle CMD}=\frac{1}{2}CD\cdot MM_{1}=\frac{1}{2}CD((1-p)AA_{1}+pBB_{1})=
=\frac{1}{2}(1-p)CD\cdot AA_{1}+\frac{1}{2}pCD\cdot BB_{1}=
=\frac{1}{2}ND\cdot AA_{1}+\frac{1}{2}NC\cdot BB_{1}=S_{\triangle AND}+S_{\triangle BNC}.
Треугольник CLN
— общая часть треугольников CMD
и BCN
, а треугольник DKN
— общая часть треугольников CMD
и ADN
, поэтому
S_{KMLN}=S_{\triangle CMD}-S_{\triangle CLN}-S_{\triangle DKN}=
=(S_{\triangle AND}+S_{\triangle BNC})-S_{\triangle CLN}-S_{\triangle DKN}=
=(S_{\triangle AND}-S_{\triangle DKN})+(S_{\triangle BNC}-S_{\triangle CLN})=S_{\triangle ADK}+S_{\triangle BCL}.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 4.20
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.20, с. 84
