2903. На стороне AB
четырёхугольника ABCD
взяты точки A_{1}
и B_{1}
, а на стороне CD
— точки C_{1}
и D_{1}
, причём AA_{1}=BB_{1}=pAB
и CC_{1}=DD_{1}=pCD
, где p\lt\frac{1}{2}
. Докажите, что \frac{S_{A_{1}B_{1}C_{1}D_{1}}}{S_{ABCD}}=1-2p
.
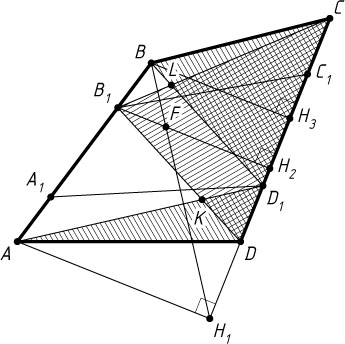
Решение. Пусть H_{1}
, H_{2}
и H_{3}
— проекции точек соответственно A
, B_{1}
и B
на прямую CD
, F
— точка пересечения отрезков BH_{1}
и B_{1}H_{2}
. Тогда
B_{1}H_{2}=B_{1}F+FH_{2}=AH_{1}\cdot\frac{BB_{1}}{AB}+BH_{3}\cdot\frac{AB_{1}}{AB}=pAH_{1}+(1-p)BH_{3}.
Поэтому
S_{\triangle CB_{1}D}=\frac{1}{2}CD\cdot BH_{2}=\frac{1}{2}CD(pAH_{1}+(1-p)BH_{3})=
=\frac{1}{2}pCD\cdot AH_{1}+\frac{1}{2}(1-p)CD\cdot BH_{3}=
=\frac{1}{2}DD_{1}\cdot AH_{1}+\frac{1}{2}CD_{1}\cdot BH_{3}=S_{\triangle ADD_{1}}+S_{\triangle BCD_{1}}.
Пусть отрезки AD_{1}
и DB_{1}
пересекаются в точке K
, а отрезки BD_{1}
и CB_{1}
— в точке L
. Треугольник CLD_{1}
— общая часть треугольников CB_{1}D
и BCD_{1}
, а треугольник DKD_{1}
— общая часть треугольников CB_{1}D
и ADD_{1}
, поэтому
S_{KB_{1}LD_{1}}=S_{\triangle CB_{1}D}-S_{\triangle CLD_{1}}-S_{\triangle DKD_{1}}=(S_{\triangle ADD_{1}}+S_{\triangle BCD_{1}})-S_{\triangle CLD_{1}}-S_{\triangle DKD_{1}}=
=(S_{\triangle ADD_{1}}-S_{\triangle DKD_{1}})+(S_{\triangle BCD_{1}}-S_{\triangle CLD_{1}})=S_{\triangle ADK}+S_{\triangle BCL}.
Следовательно,
S_{ABCD}=S_{\triangle CB_{1}D}+S_{\triangle AKD}+S_{\triangle AKB_{1}}+S_{\triangle BLB_{1}}+S_{\triangle BLC}=
=S_{\triangle CB_{1}D}+(S_{\triangle AKD}+S_{\triangle BLC})+(S_{\triangle AKB_{1}}+S_{\triangle BLB_{1}})=
=S_{\triangle CB_{1}D}+S_{KB_{1}LD_{1}}+(S_{\triangle AKB_{1}}+S_{\triangle BLB_{1}})=
=S_{\triangle CB_{1}D}+S_{\triangle AD_{1}B}.
Тогда
S_{A_{1}B_{1}C_{1}D_{1}}=S_{\triangle A_{1}B_{1}D_{1}}+S_{\triangle C_{1}D_{1}B_{1}}=
=\frac{A_{1}B_{1}}{AB}S_{\triangle AD_{1}B}+\frac{C_{1}D_{1}}{CD}S_{\triangle CB_{1}D}=(1-2p)S_{\triangle AD_{1}B}+(1-2p)S_{\triangle CB_{1}D}=
=(1-2p)(S_{\triangle AD_{1}B}+S_{\triangle CB_{1}D})=(1-2p)S_{ABCD}.
Что и требовалось доказать.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 4.21
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.21, с. 84
