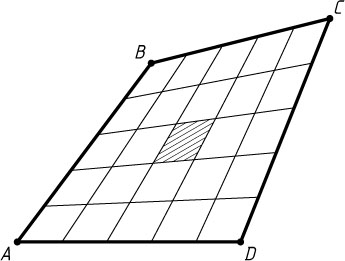
2904. Каждая из сторон выпуклого четырёхугольника разделена на пять равных частей, и соответствующие точки противоположных сторон соединены. Докажите, что площадь среднего (заштрихованного) четырёхугольника в 25 раз меньше площади исходного.
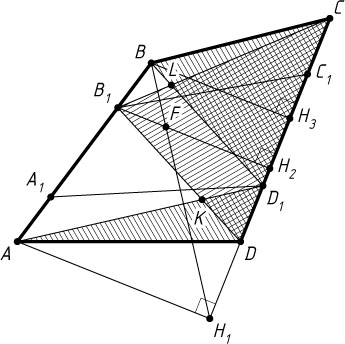
Решение. Лемма 1. На стороне AB
четырёхугольника ABCD
взяты точки A_{1}
и B_{1}
, а на стороне CD
— точки C_{1}
и D_{1}
(рис. 1), причём AA_{1}=BB_{1}=pAB
и CC_{1}=DD_{1}=pCD
, где p\lt\frac{1}{2}
. Тогда \frac{S_{A_{1}B_{1}C_{1}D_{1}}}{S_{ABCD}}=1-2p
.
Доказательство. Пусть H_{1}
, H_{2}
и H_{3}
— проекции точек соответственно A
, B_{1}
и B
на прямую CD
, F
— точка пересечения отрезков BH_{1}
и B_{1}H_{2}
. Тогда
B_{1}H_{2}=B_{1}F+FH_{2}=AH_{1}\cdot\frac{BB_{1}}{AB}+BH_{3}\cdot\frac{AB_{1}}{AB}=pAH_{1}+(1-p)BH_{3}.
Поэтому
S_{\triangle CB_{1}D}=\frac{1}{2}CD\cdot BH_{2}=\frac{1}{2}CD(pAH_{1}+(1-p)BH_{3})=
=\frac{1}{2}pCD\cdot AH_{1}+\frac{1}{2}(1-p)CD\cdot BH_{3}=
=\frac{1}{2}DD_{1}\cdot AH_{1}+\frac{1}{2}CD_{1}\cdot BH_{3}=S_{\triangle ADD_{1}}+S_{\triangle BCD_{1}}.
Пусть отрезки AD_{1}
и DB_{1}
пересекаются в точке K
, а отрезки BD_{1}
и CB_{1}
— в точке L
. Треугольник CLD_{1}
— общая часть треугольников CB_{1}D
и BCD_{1}
, а треугольник DKD_{1}
— общая часть треугольников CB_{1}D
и ADD_{1}
, поэтому
S_{KB_{1}LD_{1}}=S_{\triangle CB_{1}D}-S_{\triangle CLD_{1}}-S_{\triangle DKD_{1}}=(S_{\triangle ADD_{1}}+S_{\triangle BCD_{1}})-S_{\triangle CLD_{1}}-S_{\triangle DKD_{1}}=
=(S_{\triangle ADD_{1}}-S_{\triangle DKD_{1}})+(S_{\triangle BCD_{1}}-S_{\triangle CLD_{1}})=S_{\triangle ADK}+S_{\triangle BCL}.
Следовательно,
S_{ABCD}=S_{\triangle CB_{1}D}+S_{\triangle AKD}+S_{\triangle AKB_{1}}+S_{\triangle BLB_{1}}+S_{\triangle BLC}=
=S_{\triangle CB_{1}D}+(S_{\triangle AKD}+S_{\triangle BLC})+(S_{\triangle AKB_{1}}+S_{\triangle BLB_{1}})=
=S_{\triangle CB_{1}D}+S_{KB_{1}LD_{1}}+(S_{\triangle AKB_{1}}+S_{\triangle BLB_{1}})=
=S_{\triangle CB_{1}D}+S_{\triangle AD_{1}B}.
Тогда
S_{A_{1}B_{1}C_{1}D_{1}}=S_{\triangle A_{1}B_{1}D_{1}}+S_{\triangle C_{1}D_{1}B_{1}}=
=\frac{A_{1}B_{1}}{AB}S_{\triangle AD_{1}B}+\frac{C_{1}D_{1}}{CD}S_{\triangle CB_{1}D}=(1-2p)S_{\triangle AD_{1}B}+(1-2p)S_{\triangle CB_{1}D}=
=(1-2p)(S_{\triangle AD_{1}B}+S_{\triangle CB_{1}D})=(1-2p)S_{ABCD}.
Что и требовалось доказать.
Лемма 2. Точки X
, Y
, Z
, T
расположены соответственно на сторонах AB
, BC
, CD
и AD
выпуклого четырёхугольника ABCD
, причём \frac{AX}{XB}=\frac{DZ}{ZC}=\alpha
, \frac{AT}{TD}=\frac{BY}{YC}=\beta
. Тогда точка пересечения P
отрезков XZ
и TY
делит их в тех же отношениях, т. е. \frac{TP}{PY}=\alpha
, \frac{XP}{PZ}=\beta
.
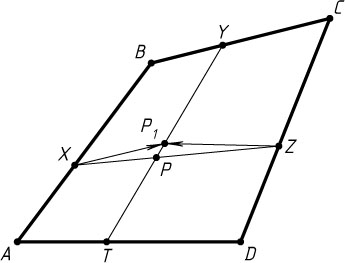
Доказательство. Пусть P_{1}
— такая точка отрезка TY
, для которой \frac{TP_{1}}{YP_{1}}=\alpha
(рис. 2). Докажем, что точка P_{1}
совпадает с точкой P
. Для этого достаточно доказать, что векторы \overrightarrow{XP_{1}}
и \overrightarrow{ZP_{1}}
коллинеарны. Действительно,
\overrightarrow{XP_{1}}=\overrightarrow{XA}+\overrightarrow{AT}+\overrightarrow{TP_{1}},~\overrightarrow{XP_{1}}=\overrightarrow{XB}+\overrightarrow{BY}+\overrightarrow{YP_{1}}.
Умножим обе части второго из этих равенств на \alpha
и сложим почленно полученное равенство с первым. Тогда
(1+\alpha)\overrightarrow{XP_{1}}=(\overrightarrow{XA}+\alpha\overrightarrow{XB})+(\overrightarrow{AT}+\alpha\overrightarrow{BY})+(\overrightarrow{TP_{1}}+\alpha\overrightarrow{YP_{1}})=
=\overrightarrow{0}+\overrightarrow{AT}+\alpha\overrightarrow{BY}+\overrightarrow{0}=\overrightarrow{AT}+\alpha\overrightarrow{BY},
откуда
\overrightarrow{XP_{1}}=\frac{1}{1+\alpha}\overrightarrow{AT}+\frac{\alpha}{1+\alpha}\overrightarrow{BY}=-\frac{\beta}{1+\alpha}\overrightarrow{DT}-\frac{\alpha\beta}{1+\alpha}\overrightarrow{CY}.
Аналогично находим, что
\overrightarrow{ZP_{1}}=\frac{1}{1+\alpha}\overrightarrow{DT}+\frac{\alpha}{1+\alpha}\overrightarrow{CY}.
Поэтому \overrightarrow{XP_{1}}=-\beta\overrightarrow{ZP_{1}}
, т. е. векторы \overrightarrow{XP_{1}}
и \overrightarrow{ZP_{1}}
коллинеарны. Следовательно, точки P
и P_{1}
совпадают и \frac{TP}{PY}=\alpha
, \frac{XP}{PZ}=\beta
. Что и требовалось доказать.
Перейдём к нашей задаче (рис. 3). По лемме 1 площадь среднего из четырёхугольников, заданных отрезками, соединяющими точки сторон AB
и CD
, в пять раз меньше площади исходного четырёхугольника. Из леммы 2 следует, что каждый из отрезков, соединяющих соответствующие точки деления на сторонах AB
и CD
, делится отрезками, соединяющими соответствующие точки деления на сторонах BC
и AD
, на пять равных частей. Тогда по лемме 1 площадь внутреннего четырёхугольника равна \frac{1}{5}\cdot\frac{1}{5}=\frac{1}{25}
площади четырёхугольника ABCD
.

Примечание. 1. Доказательство леммы 2 с использованием понятия центра тяжести (Квант, 1976, N9, с.49).
Расположим в точках A
, B
, C
, D
грузы с массами 1, \alpha
, \alpha\beta
и \beta
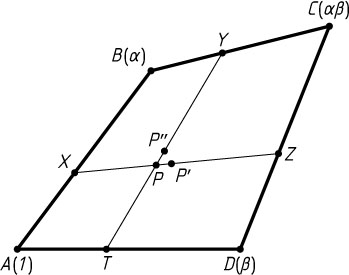
соответственно и найдём двумя способами центр тяжести этих четырёх грузов (рис. 4).
Центр тяжести грузов A(1)
и B(\alpha)
лежит в точке X
, грузов D(\beta)
и C(\alpha\beta)
— в точке Z
. Значит, центр тяжести всех четырёх грузов лежит в точке P'
, делящей отрезок XZ
в отношении
\frac{XP'}{P'Z}=\frac{\beta+\alpha\beta}{1+\alpha}=\beta.
Аналогично, объединяя в пары грузы A(1)
и D(\beta)
, B(\alpha)
и C(\alpha\beta)
, докажем, что центр тяжести этих грузов лежит в точке P''
отрезка TY
, для которой \frac{TP''}{P''Y}=\alpha
.
Поскольку центр тяжести принадлежит и XZ
, и TY
, то он должен совпадать с точкой пересечения этих отрезков, т. е. точки P'
, P''
и P
совпадают.
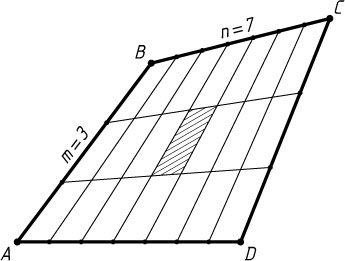
2. Верно более общее утверждение. Если стороны AB
и CD
выпуклого четырёхугольника ABCD
разделены на m
, а стороны BC
и AD
— на n
равных частей (m
и n
нечётны; рис. 5), то площадь «центрального» четырёхугольника в m\cdot n
раз меньше площади четырёхугольника ABCD
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 4.21
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.22, с. 84
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 333, с. 39





