2905. Точка O
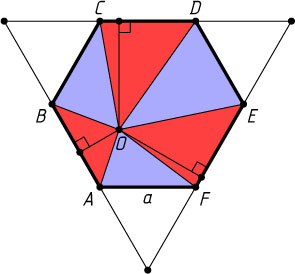
, лежащая внутри правильного шестиугольника, соединена с вершинами. Возникшие при этом шесть треугольников раскрашены попеременно в красный и синий цвет. Докажите, что сумма площадей красных треугольников равна сумме площадей синих.
Решение. Пусть сторона правильного шестиугольника равна a
. Прямые, содержащие стороны шестиугольника, принадлежащие красным треугольникам, задают равносторонний треугольник со стороной 3a
. Сумма расстояний от точки O
до сторон этого треугольника равна высоте равностороннего треугольника, т. е. \frac{3a\sqrt{3}}{2}
. С другой стороны, это сумма высот, проведённых из общей вершины O
красных треугольников, значит, сумма площадей красных треугольников равна \frac{1}{2}\cdot a\cdot\frac{3a\sqrt{3}}{2}=\frac{3a^{2}\sqrt{3}}{4}
. Аналогично, сумма площадей синих треугольников также равна \frac{3a^{2}\sqrt{3}}{4}
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 4.28
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.28, с. 84
