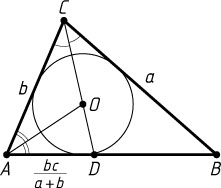
2906. В треугольнике ABC
известно, что AB=c
, BC=a
, AC=b
. В каком отношении центр вписанной окружности треугольника делит биссектрису CD
?
Ответ. \frac{a+b}{c}
.
Решение. По свойству биссектрисы треугольника \frac{AD}{BD}=\frac{AC}{BC}=\frac{b}{a}
, а так как AB=c
, то
AD=b\cdot\frac{c}{a+b}=\frac{bc}{a+b}.
Пусть O
— центр вписанной окружности треугольника ABC
. Тогда O
— точка пересечения биссектрис треугольника, поэтому AO
— биссектриса треугольника ACD
. Следовательно,
\frac{CO}{OD}=\frac{AC}{AD}=\frac{b}{\frac{bc}{a+b}}=\frac{a+b}{c}.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 26, с. 7
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.10, с. 46
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.17(б), с. 13
