2914. На сторонах AB
и BC
параллелограмма ABCD
расположены точки N
и M
соответственно, причём AN:NB=3:2
, BM:MC=2:5
. Прямые AM
и DN
пересекаются в точке O
. Найдите отношения OM:OA
и ON:OD
.
Ответ. 20:21
; 6:35
Указание. Продолжите DN
до пересечения с прямой BC
и рассмотрите две пары подобных треугольников.
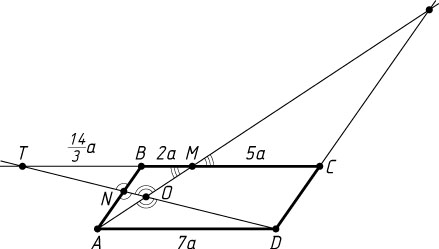
Решение. Продолжим DN
до пересечения с прямой BC
в точке T
. Положим BM=6a
, CM=15a
. Из подобия треугольников TNB
и DNA
(коэффициент \frac{2}{3}
) находим, что
TB=\frac{2}{3}AD=\frac{2}{3}BC=\frac{2}{3}\cdot21a=14a,
а из подобия треугольников TOM
и DOA
—
\frac{OM}{OA}=\frac{TM}{AD}=\frac{14a+6a}{21a}=\frac{20}{21}.
Аналогично находим, что \frac{ON}{OD}=\frac{6}{35}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.5, с. 46
