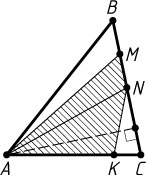
2925. Точки M
и N
расположены на стороне BC
треугольника ABC
, а точка K
— на стороне AC
, причём BM:MN:NC=1:1:2
и CK:AK=1:4
. Известно, что площадь треугольника ABC
равна 1. Найдите площадь четырёхугольника AMNK
.
Ответ. \frac{13}{20}
.
Решение. У треугольников AMB
и ABC
общая высота, проведённая из вершины A
, поэтому их площади относятся как основания, значит,
S_{\triangle AMB}=\frac{BM}{BC}\cdot S_{\triangle ABC}=\frac{1}{4}\cdot1=\frac{1}{4}.
Аналогично,
S_{\triangle ANC}=\frac{1}{2},~S_{\triangle CNK}=\frac{CK}{AC}\cdot S_{\triangle ANC}=\frac{1}{5}\cdot\frac{1}{2}=\frac{1}{10}.
Следовательно,
S_{AMNK}=S_{\triangle ABC}-S_{\triangle AMC}-S_{\triangle CNK}=1-\frac{1}{4}-\frac{1}{10}=1-\frac{7}{20}=\frac{13}{20}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 7.2, с. 52
