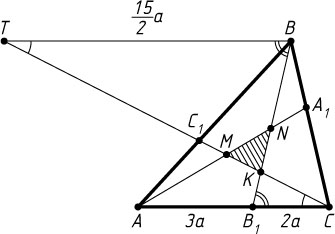
2929. На сторонах BC
, AC
и AB
треугольника ABC
расположены точки A_{1}
, B_{1}
и C_{1}
соответственно, причём BA_{1}:A_{1}C=CB_{1}:B_{1}A=AC_{1}:C_{1}B=2:3
. Найдите площадь треугольника, образованного пересечениями прямых AA_{1}
, BB_{1}
и CC_{1}
, если известно, что площадь треугольника ABC
равна 1.
Ответ. \frac{1}{19}
.
Указание. Найдите отношение, в котором делятся точкой пересечения отрезки BB_{1}
и CC_{1}
.
Решение. Пусть K
— точка пересечения отрезков BB_{1}
и CC_{1}
. Через точку B
проведём прямую, параллельную AC
, и продолжим CC_{1}
до пересечения с этой прямой в точке T
. Положим CB_{1}=2a
, AB_{1}=3a
Треугольники BC_{1}T
и AC_{1}C
подобны с коэффициентом \frac{3}{2}
. Поэтому BT=\frac{3}{2}AC=\frac{3}{2}5a=\frac{15}{2}a
, а из подобия треугольников BKT
и B_{1}KC
находим, что
\frac{BK}{KB_{1}}=\frac{BT}{CB_{1}}=\frac{\frac{15}{2}a}{2a}=\frac{15}{4}.
Поэтому
S_{\triangle CB_{1}K}=\frac{4}{19}S_{\triangle CBB_{1}}=\frac{4}{19}\cdot\frac{2}{5}S_{\triangle ABC}=\frac{8}{95}.
Аналогично находим, что
S_{\triangle AMC_{1}}=S_{\triangle BNA_{1}}=\frac{8}{95},
где M
— точка пересечения AA_{1}
и CC_{1}
, а N
— BB_{1}
и AA_{1}
. Следовательно,
S_{\triangle MNK}=S_{\triangle ABC}-S_{\triangle ABA_{1}}-S_{\triangle BCB_{1}}-S_{\triangle CAC_{1}}+S_{\triangle CB_{1}K}+S_{\triangle AC_{1}M}+S_{\triangle BA_{1}N}=
=1-\frac{2}{5}-\frac{2}{5}-\frac{2}{5}+\frac{8}{95}+\frac{8}{95}+\frac{8}{95}=1-\frac{6}{5}+\frac{24}{95}=\frac{24}{95}-\frac{1}{5}=\frac{1}{19}.