2936. Точки M
и N
расположены на боковых сторонах соответственно AB
и CD
трапеции ABCD
, причём MN\parallel AD
. Известно, что площадь трапеции MBCN
относится к площади трапеции AMND
как 2:3
. Найдите MN
, если BC=a
, AD=b
.
Ответ. \sqrt{\frac{3a^{2}+2b^{2}}{5}}
.
Указание. С помощью дополнительных построений получите подобные треугольники.
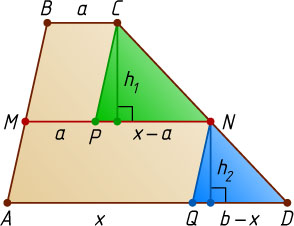
Решение. Первый способ. Пусть P
— точка пересечения с MN
прямой, проходящей через точку C
параллельно AB
, Q
— точка пересечения с AD
прямой, проходящей через точку N
параллельно AB
. Обозначим MN=x
; h_{1}
и h_{2}
— высоты подобных треугольников PCN
и QND
(рис. 1).
Пусть b\gt a
. Отношение площадей трапеций BMNC
и MADN
равно 2:3
, поэтому
(x+a)h_{1}=\frac{2}{3}\cdot(b+x)h_{2},
откуда \frac{h_{1}}{h_{2}}=\frac{2}{3}\cdot\frac{b+x}{x+a}
.
Из подобия треугольников CPN
и NQD
следует, что \frac{h_{1}}{h_{2}}=\frac{x-a}{b-x}
. Поэтому
\frac{2}{3}\cdot\frac{b+x}{x+a}=\frac{x-a}{b-x}.
Из этого уравнения находим, что x=\sqrt{\frac{3a^{2}+2b^{2}}{5}}
.
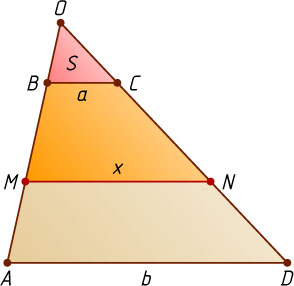
Второй способ. Пусть O
— точка пересечения продолжений боковых сторон AB
и DC
(рис. 2), S
— площадь треугольника BOC
, MN=x
— искомый отрезок. Тогда S_{\triangle MNO}-S=\frac{2}{3}(S_{\triangle AOD}-S_{\triangle MNO})
, или
\frac{x^{2}}{a^{2}}\cdot S-S=\frac{2}{3}\left(\frac{b^{2}}{a^{2}}\cdot S-\frac{x^{2}}{a^{2}}\cdot S\right).
Отсюда находим, что x^{2}=\frac{3a^{2}+2b^{2}}{2}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.15, с. 112

