2938. Найдите радиусы вписанной и вневписанных окружностей треугольника со сторонами 3, 4, 5.
Ответ. 1; 2; 3; 6.
Решение. Рассмотрим треугольник ABC
, в котором AB=5
, BC=3
, AC=4
. Поскольку AB^{2}=5^{2}=4^{2}+3^{2}=AC^{2}+BC^{2}
, этот треугольник — прямоугольный, причём AB
— его гипотенуза. Если A_{1}
, B_{1}
и C_{1}
— точки касания окружности, вписанной в треугольник, со сторонами BC
, AC
и AB
соответственно, а r
— радиус вписанной окружности с центром O
, то четырёхугольник OA_{1}CB_{1}
квадрат со стороной r
, поэтому
AC_{1}=AB_{1}=AC-CB_{1}=AC-r,~BC_{1}=BA_{1}=BC-CA_{1}=BC-r.
Тогда
AB=AC_{1}+BC_{1}=(AC-r)+(BC-r)=AC+BC-2r.
Следовательно,
r=\frac{AC+BC-AB}{2}=\frac{4+3-5}{2}=1.
Пусть p=\frac{3+4+5}{2}=6
— полупериметр треугольника ABC
, r_{a}
— радиус окружности с центром O_{a}
, касающейся катета BC
в точке A_{2}
, а продолжений гипотенузы AB
и катета AC
— в точках M
и N
соответственно. Тогда
2p=AC+BC+AB=AC+(CA_{2}+C_{2}B)+AB=
=AC+(CN+BM)+AB=(AC+CN)+(AB+BM)=AN+AM,
а так как AM=AN
, то AN=p
. Четырёхугольник O_{a}NCA_{2}
— квадрат со стороной r_{a}
, поэтому
r_{a}=O_{a}A_{2}=CN=AN-AC=p-AC=6-4=2.
Если r_{b}
и r_{c}
— радиусы вневписанных окружностей треугольника ABC
, касающихся катета AC
и гипотенузы AB
, то аналогично найдём, что
r_{b}=p-BC=6-3=3,~r_{c}=p=6.
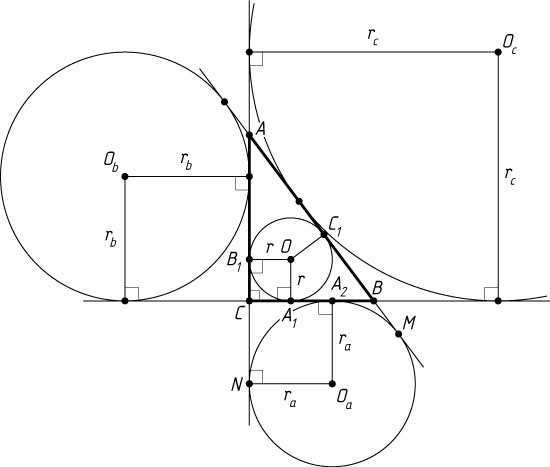
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.5, с. 86
