2949. Внутри круга радиуса 15 взята точка M
на расстоянии 13 от центра. Через точку M
проведена хорда, равная 18. Найдите отрезки, на которые делится хорда точкой M
.
Ответ. 4 и 14.
Указание. Опустите перпендикуляр из центра окружности на данную хорду.
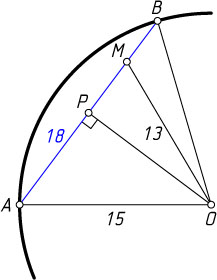
Решение. Первый способ. Пусть O
— центр данной окружности (рис. 1), AB
— данная хорда, AB=18
, OM=13
. Пусть P
— основание перпендикуляра, опущенного из центра O
на хорду AB
. Тогда P
— середина AB
и
OP=\sqrt{OA^{2}-AP^{2}}=\sqrt{15^{2}-9^{2}}=12,
PM=\sqrt{OM^{2}-OP^{2}}=\sqrt{13^{2}-12^{2}}=5.
Если точка P
расположена между M
и A
, то
AM=AP+PM=9+5=14,~BM=BP-PM=18-14=4.
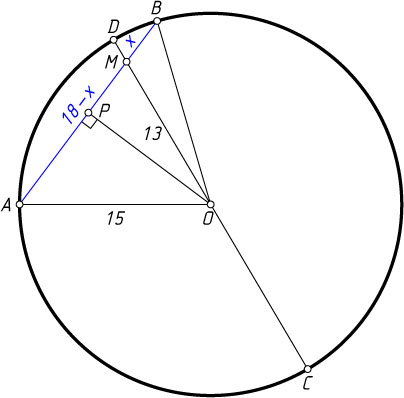
Второй способ. Пусть O
— центр окружности (рис. 2), AB
— данная хорда. Проведём диаметр CD
, содержащий точку M
(M
между O
и D
). Обозначим MB=x
. Тогда
AM=18-x,~DM=OD-OM=15-13=2;
MC=OM+OC=13+15=28,~AM\cdot MB=MD\cdot MC,
или
(18-x)x=2\cdot28.
Из этого уравнения находим, что x=4
или x=14
.
