2958. Четыре окружности попарно касаются внешним образом (в шести различных точках). Пусть a
, b
, c
, d
— их радиусы, \alpha=\frac{1}{a}
, \beta=\frac{1}{b}
, \gamma=\frac{1}{c}
, \delta=\frac{1}{d}
. Докажите, что
2(\alpha^{2}+\beta^{2}+\gamma^{2}+\delta^{2})=(\alpha+\beta+\gamma+\delta)^{2}.
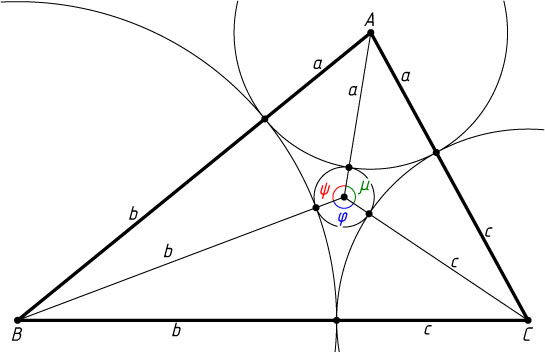
Решение. Пусть A
, B
, C
, D
— центры данных окружностей радиусов a
, b
, c
, d
соответственно. Тогда
AB=a+b,~BC=b+c,~AC=a+c,~BD=b+d,~CD=c+d.
Обозначим \angle BDC=\varphi
, \angle ADB=\psi
, \angle ADC=\mu
. По теореме косинусов
\cos\varphi=\frac{BD^{2}+CD^{2}-BC^{2}}{2BD\cdot CD}=\frac{(b+d)^{2}+(c+d)^{2}-(b+c)^{2}}{2(b+d)(c+d)}=
=\frac{d^{2}+bd+cd-bc}{(b+d)(c+d)}.
Тогда
\cos^{2}\frac{\varphi}{2}=\frac{1+\cos\varphi}{2}=\frac{bc+bd+cd+2d^{2}+bd+cd-bc}{2(b+d)(c+d)}=
=\frac{d(b+c+d)}{(b+d)(c+d)},
\sin^{2}\frac{\varphi}{2}=\frac{1-\cos\varphi}{2}=\frac{bc}{(b+d)(c+d)}.
Аналогично,
\sin^{2}\frac{1}{2}\angle ADB=\sin^{2}\frac{\psi}{2}=\frac{ab}{(b+d)(a+d)},
\sin^{2}\frac{1}{2}\angle ADC=\sin^{2}\frac{\mu}{2}=\frac{ac}{(a+d)(c+d)}.
Так как \varphi+\psi+\mu=360^{\circ}
, то \frac{\varphi}{2}+\frac{\psi}{2}+\frac{\mu}{2}=180^{\circ}
. Рассмотрим треугольник с углами \frac{\varphi}{2}
, \frac{\psi}{2}
, \frac{\mu}{2}
. Пусть R
— радиус описанной окружности этого треугольника. Тогда стороны треугольника равны 2R\sin\frac{\varphi}{2}
, 2R\sin\frac{\psi}{2}
, 2R\sin\frac{\mu}{2}
. По теореме косинусов
4R^{2}\sin^{2}\frac{\varphi}{2}=4R^{2}\sin^{2}\frac{\psi}{2}+4R^{2}\sin^{2}\frac{\mu}{2}-8R^{2}\sin\frac{\psi}{2}\sin\frac{\mu}{2}\cos\frac{\varphi}{2},
\sin^{2}\frac{\varphi}{2}-\sin^{2}\frac{\psi}{2}-\sin^{2}\frac{\mu}{2}+2\sin\frac{\psi}{2}\sin\frac{\mu}{2}\cos\frac{\varphi}{2}=0,
\frac{bc}{(b+d)(c+d)}-\frac{ab}{(b+d)(a+d)}-\frac{ac}{(a+d)(c+d)}+
+2\sqrt{\frac{ab}{(b+d)(a+d)}}\cdot\sqrt{\frac{ac}{(a+d)(c+d)}}\cdot\sqrt{\frac{d(b+c+d)}{(b+d)(c+d)}}=0,
\frac{a+d}{a}-\frac{c+d}{c}-\frac{b+d}{b}+2\sqrt{\frac{d(b+c+d)}{bc}}=0,
1+\frac{d}{a}-1-\frac{d}{c}-1-\frac{d}{b}+2\sqrt{d\left(\frac{1}{c}+\frac{1}{b}+\frac{d}{bc}\right)}=0,
-1+\frac{d}{a}-\frac{d}{c}-\frac{d}{b}+2\sqrt{d\left(\frac{1}{c}+\frac{1}{b}+\frac{d}{bc}\right)}=0,
Разделив обе части этого равенства на d
, получим, что
-\frac{1}{d}+\frac{1}{a}-\frac{1}{c}-\frac{1}{b}+2\sqrt{\frac{1}{dc}+\frac{1}{db}+\frac{1}{bc}}=0,
\alpha-\beta-\gamma-\delta+2\sqrt{\gamma\delta+\beta\delta+\beta\gamma}=0,~\beta+\gamma+\delta-\alpha=2\sqrt{\gamma\delta+\beta\delta+\beta\gamma},
(\beta+\gamma+\delta-\alpha)^{2}=4(\gamma\delta+\beta\delta+\beta\gamma),
(\beta+\gamma+\delta)^{2}-2\alpha(\beta+\gamma+\delta)+\alpha^{2}=4(\gamma\delta+\beta\delta+\beta\gamma),
\beta^{2}+\gamma^{2}+\delta^{2}+2\beta\gamma+2\beta\delta+2\gamma\delta-2\alpha\beta-2\alpha\gamma-2\alpha\delta+\alpha^{2}=4\gamma\delta+4\beta\delta+4\beta\gamma,
\alpha^{2}+\beta^{2}+\gamma^{2}+\delta^{2}=2\beta\gamma+2\beta\delta+2\gamma\delta+2\alpha\beta+2\alpha\gamma+2\alpha\delta,
2\alpha^{2}+2\beta^{2}+2\gamma^{2}+2\delta^{2}=\alpha^{2}+\beta^{2}+\gamma^{2}+\delta^{2}+2\beta\gamma+2\beta\delta+2\gamma\delta+2\alpha\beta+2\alpha\gamma+2\alpha\delta,
откуда
2(\alpha^{2}+\beta^{2}+\gamma^{2}+\delta^{2})=(\alpha+\beta+\gamma+\delta)^{2}.
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — № 1.57, с. 29-31
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.23(б)
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.24(б), с. 59
