2969. Центры O_{1}
, O_{2}
и O_{3}
трёх непересекающихся окружностей одинакового радиуса расположены в вершинах треугольника. Из точек O_{1}
, O_{2}
и O_{3}
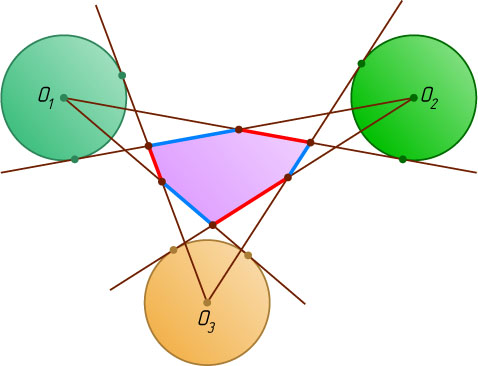
проведены касательные к данным окружностям так, как показано на рисунке. Известно, что эти касательные, пересекаясь, образовали выпуклый шестиугольник, стороны которого через одну покрашены в красный и синий цвет. Докажите, что сумма длин красных отрезков равна сумме длин синих отрезков.
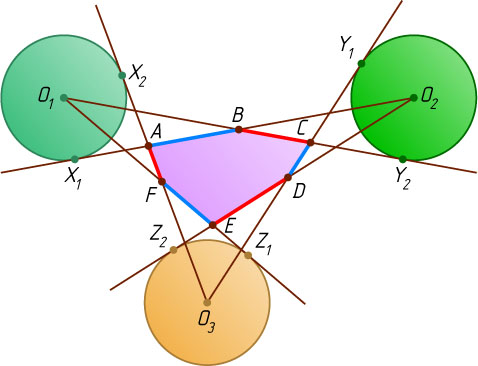
Решение. Обозначим точки касания через X_{1}
, X_{2}
, Y_{1}
, Y_{2}
, Z_{1}
, Z_{2}
, а вершины шестиугольника — A
, B
, C
, D
, E
и F
. Радиусы окружностей одинаковы, поэтому
X_{1}O_{2}=O_{1}Y_{2},~Y_{1}O_{3}=O_{2}Z_{2},~Z_{1}O_{1}=O_{3}X_{2},
или
X_{1}A+AB+BO_{2}=O_{1}B+BC+CY_{2},
Y_{1}C+CD+DO_{3}=O_{2}D+DE+EZ_{2},
Z_{1}E+EF+FO_{1}=O_{3}F+FA+AX_{2}.
Сложив почленно полученные равенства и заметив, что
X_{1}A=AX_{2},~Y_{1}C=CY_{2},~Z_{1}E=EZ_{2}
(как отрезки касательных, проведённых к окружности из одной точки) и
BO_{2}=O_{1}B,~DO_{3}=O_{2}D,~FO_{1}=O_{3}F
(так как радиусы данных окружностей равны), получим, что
AB+CD+EF=BC+DE+FA,
что и требовалось доказать.
Автор: Терёшин Д. А.
Источник: Всероссийская олимпиада школьников. — 1995-96, XXII, заключительный этап, 9 класс
Источник: Агаханов Н. Х. и др. Всероссийские математические олимпиады школьников. 1993—2006. — М.: МЦНМО, 2007. — № 498, с. 64

